Difference between revisions of "Inline oscillating cylinder by Michael Alletto"
Jozsef Nagy (talk | contribs) (Created page with "category:mesh * '''contributor''': Michael Alletto * '''affiliation''': WRD MS * '''contact''': <mail address='michael.alletto@gmx.de' description='author'>click here for...") |
Jozsef Nagy (talk | contribs) |
||
| Line 24: | Line 24: | ||
One of this phenomena are frequency lock in: When the frequency of the oscillating cylinder is close to twice the shedding frequency of the stationary cylinder f<sub>st</sub>, the frequency of the vortices shed became equal to the one of the cylinder. The amplitude of the cylinder motion which is required to maintain the lock in regime is increasing with departure from twice the shedding frequency of a fixed cylinder [2]. | One of this phenomena are frequency lock in: When the frequency of the oscillating cylinder is close to twice the shedding frequency of the stationary cylinder f<sub>st</sub>, the frequency of the vortices shed became equal to the one of the cylinder. The amplitude of the cylinder motion which is required to maintain the lock in regime is increasing with departure from twice the shedding frequency of a fixed cylinder [2]. | ||
| − | Another interesting phenomena is the increase of the lift coefficient C<sub>l</sub> when the cylinder is oscillating at 2f<sub>st</sub> [6]. For frequencies which are either lower or higher than 2f<sub>st</sub> C<sub>l</sub> is much lower [6]. [3] made simulations with an in line oscillating cylinder at a Reynolds number of Re = 175. For this Re number the ow around a | + | Another interesting phenomena is the increase of the lift coefficient C<sub>l</sub> when the cylinder is oscillating at 2f<sub>st</sub> [6]. For frequencies which are either lower or higher than 2f<sub>st</sub> C<sub>l</sub> is much lower [6]. [3] made simulations with an in line oscillating cylinder at a Reynolds number of Re = 175. For this Re number the ow around a fixed cylinder is two dimensional. For an oscillation frequency f<sub>c</sub> of 2f<sub>st</sub> and an amplitude of 65% of the cylinder diameter the frequency spectrum of the lift force increases considerably. For lower amplitudes of the oscillation only a few peaks are present in the frequency spectrum. |
| − | In order to simulate this kind of ow | + | In order to simulate this kind of ow congurations, OpenFOAM offers two different approaches: the overset methodology and the morphing mesh method. The latter can be used if the cylinder motion is not to large to deteriorate the mesh quality. Regarding the overset method we have one or more meshes which displace relative to a background mesh. The coupling between the moving meshes and the background mesh is achieved via interpolation of the |
ow quantities. Regarding the morphing mesh, the connectivity between the cells remain unchanged.However the position of the points building a cell can move relative to each other. | ow quantities. Regarding the morphing mesh, the connectivity between the cells remain unchanged.However the position of the points building a cell can move relative to each other. | ||
Revision as of 05:52, 9 April 2020
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v1912
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to Collection by authors.
Go back to Meshing.
Go back to Turbulence.
Contents
2D flapping wing
You can download the case file OscillatingCylinderSend.tar.gz here.
Introduction
In this tutorial we will examine the inline oscillatory motion of a cylinder in a uniform ow. Inline means that the cylinder is oscillating parallel to the incoming flow. This kind of configuration is often used to validate solvers aiming to simulate large body motions (see e.g. [1, 4, 5]). The reason is that that despite its simplicity this configuration is associated with a variety of complex physical phenomena.
One of this phenomena are frequency lock in: When the frequency of the oscillating cylinder is close to twice the shedding frequency of the stationary cylinder fst, the frequency of the vortices shed became equal to the one of the cylinder. The amplitude of the cylinder motion which is required to maintain the lock in regime is increasing with departure from twice the shedding frequency of a fixed cylinder [2].
Another interesting phenomena is the increase of the lift coefficient Cl when the cylinder is oscillating at 2fst [6]. For frequencies which are either lower or higher than 2fst Cl is much lower [6]. [3] made simulations with an in line oscillating cylinder at a Reynolds number of Re = 175. For this Re number the ow around a fixed cylinder is two dimensional. For an oscillation frequency fc of 2fst and an amplitude of 65% of the cylinder diameter the frequency spectrum of the lift force increases considerably. For lower amplitudes of the oscillation only a few peaks are present in the frequency spectrum. In order to simulate this kind of ow congurations, OpenFOAM offers two different approaches: the overset methodology and the morphing mesh method. The latter can be used if the cylinder motion is not to large to deteriorate the mesh quality. Regarding the overset method we have one or more meshes which displace relative to a background mesh. The coupling between the moving meshes and the background mesh is achieved via interpolation of the ow quantities. Regarding the morphing mesh, the connectivity between the cells remain unchanged.However the position of the points building a cell can move relative to each other.
Since both methods described above can be used to simulate the flow of an inline oscillating cylinder, both methods can be compared against each other besides the validation against experiments and other simulations. The comparison of this two methods and the validation against experiments is the purpose of this tutorial.
Set up
The Simulation setup is inspired by the experiments of [3]. The experiments consisted in a flat plate which rotates about the stroke axis with an angle of 0 <= Φ <= 90° and pitches about the rotational axis with an angle of β = +- 50°. The details of the kinematics are described in [3]. The wing span was R = 107mm and the thickness was s = 3.4mm (see [4] since in [3] the thickness of the plate was not described). The distance from the rotational axis to the wing root was ΔR = 71.5mm (private communications). In order to perform a two--dimensional simulation, the rotatory motion of the point located at mid-span is projected on a horizontal plane. That means that the displacement of the point located at the center of the wing in the experiment is the same as the horizontal displacement of the wing in the simulation. The pitching motion is the same in the experiment and in the simulation.
Mesh generation
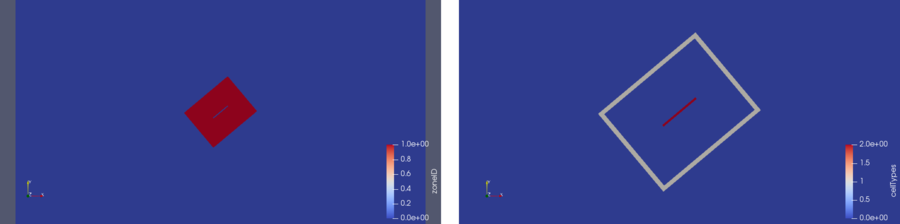
Since the interpolation errors in overset grids is proportional to the cell size difference between moving and background mesh (of course also to the cell size itself), the purpose of the mesh generation was to minimize this errors. In order to achieve this goal, the size of the cells of the background mesh and the moving grid have to be similar in the region where the interpolation is performed. For this reason the moving mesh was generated with snappyHexMesh in combination with different refinement regions. Since snappyHexMesh can perform only three--dimensional refinements (a hexahedron is split in eight cells with no option for the user to impose only splitting in two directions) the utility extrudeMesh is used. With this utility the 2D mesh at the symmetry plane can be extruded having a mesh with only one cell in span wise direction. The mesh is shown in the figure below.
Simulation set up
As for the other tutorials presented, the different zones (background mesh and the moving meshes) should be differentiated by the scalar field zoneID. This field should have a different number (starting with zero) for each mesh (see figure below). The overset method implemented in OpenFOAM detects itself the different cell types. The cells adjacent to the patch denominated as overset are chosen as interpolated. For this cells the matrix coefficients are not derived from the finite volume discretization but using one of overset interpolation method chosen by the user. The cells which are inside the wing are flagged as hole cells and exclude from the calculation. The other cells are treated as calculated (the matrix coefficients are derived from a finite volume discretization). The cell types are visualized on the right of the figure below.
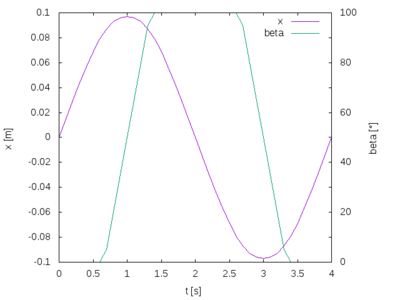
The kinematics of the wing are imposed by choosing the adequat motion solver. Since the wing executes a sinusoidal movement in x-direction and pitches at the and of the half stroke with a linear change of the angle β (see figure below on wing kinematics where the evolution of the x-position of and the angle β during the first cycle is shown), the tabulated6DoFMotion function is chosen. This function allows to impose the temporal evolution of the displacement in x-,y- and z-direction and also the rotation about the same axis. The displacements and rotation are relative to the initial position. The rotation is described about the point denoted as CofG. Since the rotation in the experiment was about an axis located a forth of the chord length from the leading edge, CofG was set to at this position in the initial state. The dynamic mesh dictionary is shown below.
dynamicFvMesh dynamicOversetFvMesh;
solver multiSolidBodyMotionSolver;
multiSolidBodyMotionSolverCoeffs
{
movingZone
{
solidBodyMotionFunction tabulated6DoFMotion;
CofG (0.00546 0.00651 0);
timeDataFileName "<constant>/6DoF.dat";
}
}
Case specific postprocessing
In the reference experiments of [3] the phase averaged lift coefficient Cl = Fy/(0.5ρU*2) and the phase averaged drag coefficient Cd = Fx/(0.5ρU*2) were measured. U* is defined as U* = πfR where f is the flapping frequency and R is the wing span. In the following simulations the force coefficients are computed by scaling the forces by the mean flapping velocity and the density. Since the forces scale with the square of the velocity, the measured force coefficients have to be rescaled by the mean flapping velocity at the second moment of area radius R2 (see e.g. [5]) to be compared with the present simulation. A small python script is included in the tutorial which computes the phase averaged force coefficients of the simulation and compares it with the measurements.
Furthermore phase averaged PIV measurements of the normalized vorticity ω = ω* c/U* where shown in the reference experiment. c represents the chord length. In order to compare this quantity with the experiments, a small coded function object is included in the controlDict which does the phase averaging at phase times of t = 0.2, 0.64, 1.24, 1.6 and 1.8 s. This times correspond to the non--dimensional times of t/T = 0.05, 0.16, 0.31, 0.4 and 0.45 of the reference experiments of [3].
Results
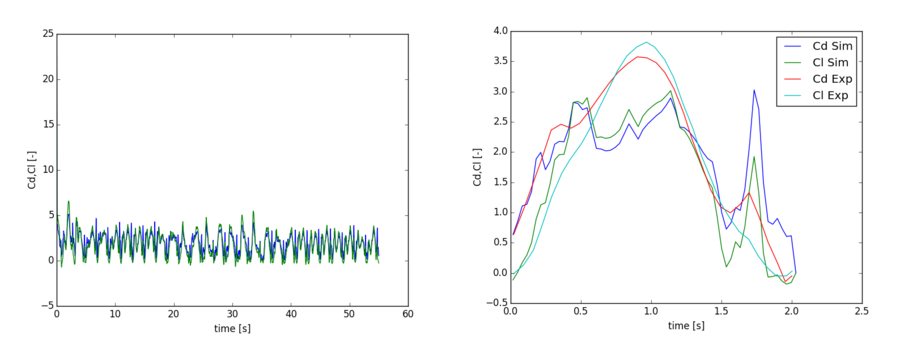
The figure below shows the temporal evolution of the force coefficient (left) and the comparison of the phase averaged force coefficients with the experiments (right). Looking at the evolution of the force coefficient it is evident that the signal is not completely periodic as expected for this low Reynolds number. The interaction of the wing with the residual vorticities from the previous strokes seems to lead to a not completely periodic evolution of the forces on the wing. The agreement of the phase averaged coefficients with the experiments is satisfactory especially if we keep in mind that a 2D simulation is compared with a 3D experiment. In the simulation the influence of the flow from the root of the wing to the tip which is induced by a mean spanwise pressure gradient is completely disregarded. The peak of the force coefficients at the end of the cycle probably results from an too high influence of the wing rotation at the end of the cycle.
According to [3] the cycle of a flapping wing can be divided into five stages: the emergence of the leading edge vortex (LEV), the growth of the LEV, the lift--off of the LEV, the breakdown and decay of the LEV. For each of this stages the phase averaged scaled vorticity ω (left column of the figure below) and the pressure scaled by the mean flapping velocity squared and the density (right column of the figure below) is shown. The interpretation of the results and its comparison with the reference experiment is left to the interested reader.
References
[1] Dominic D Chandar, Bharathi Boppana, and Vasanth Kumar. A comparative study of di�erent overset grid solvers between openfoam, star-ccm+ and ansys-fluent. In 2018 AIAA Aerospace Sciences Meeting, page 1564, 2018.
[2] Owen M Gri�n and MS Hall. Vortex shedding lock-on and flow control in bluff body wakes. 1991.
[3] Justin S Leontini, David Lo Jacono, and Mark C Thompson. A numerical study of an inline oscillating cylinder in a free stream. Journal of Fluid Mechanics, 688:551-568, 2011.
[4] Chuan-Chieh Liao, Yu-Wei Chang, Chao-An Lin, and JM McDonough. Simulating flows with moving rigid boundary using immersed-boundary method. Computers & Fluids, 39(1):152-167, 2010. 11
[5] Shen-Wei Su, Ming-Chih Lai, and Chao-An Lin. An immersed boundary technique for simulating complex flows with rigid boundary. Computers & Fluids, 36(2):313-324, 2007.
[6] Y Tanida, A Okajima, and Y Watanabe. Stability of a circular cylinder oscillating in uniform ow or in a wake. Journal of Fluid Mechanics, 61(4):769-784, 1973.
[7] Charles HK Williamson. Vortex dynamics in the cylinder wake. Annual review of Fluid mechanics, 28(1):477-539, 1996.