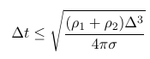Bubble growth detachment influence temporal spacial resolution Michael Alletto
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v2012
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to Collection by authors.
Contents
Bubble growth detachment influence spacial and temporal resolution
You can download the case files [1] here.
Introduction
In this tutorial we will examine the influence of the grid size and the Courant number on the flow of a bubble detaching from a flat surface. In a previous tutorial (see https://wiki.openfoam.com/Bubble_growth_detachment_influence_BC_domain_size_by_Michael_Alletto) we have analyzed the influence of the boundary conditions and the domain size on the same configuration considered here. In the previous tutorial we concluded that a domain radius of approximately 10 pipe diameter from which the bubble is released is enough to have near domain size independent solutions. Furthermore we found a suitable set of boundary conditions for which the flow we analyzed behaves as expected. This two investigation should always be done as first sensitivity studies when approaching a new configuration where one is not sure of the settings to choose. The next step to investigate a new problem should be to check the influence of the grid size and the time step size (in this case we will analyze the influence of the maximum Courant number). This two parameters are intrinsically connected to the discretization errors made. Ideally the error made compared to a known solution will approach to zero when the grid size and time step size becomes small enough (of course only if we solve the correct equation an we do not make any modeling errors). Since in our case we do not have an exact analytical solution, we expect that the change of the variable of interest (the detachment time of the bubble) will not substantially change if the grid size and time step size are small enough.
Simulation setup
The setup of the simulation was already described in https://wiki.openfoam.com/Bubble_growth_detachment_influence_BC_domain_size_by_Michael_Alletto. For this reason only the parameters important for this tutorial will be analyzed in more detail. Regarding the boundary condition the we chose the sets used together with the inflowOutflow conditions for the velocity U. The reason was that if a pressureInletOutletVelocity was used, for a fine grid backflow was observed. By choosing an inflowOutflow condition and setting the inflow velocity to zero, the backflow is prevented.
The next listing shows the fvSchemes dictionary. We used a first order Euler scheme for the temporal discretization. Regarding the convective fluxes, we used a Gauss limitedLinearV 1 scheme for the convective fluxes in the momentum equation. The limited linear schemes in openfoam limit the linear schemes towards an upwind scheme in regions of rapidly changing flow (see https://cfd.direct/openfoam/user-guide/v6-fvschemes/). The basic idea of the limited schemes (which are similar to the bounded schemes) is to avoid numerical oscillation when interpolating the variable from the cell center to the face center which are common to higher order schemes. For the tails see the book of [1]. The vanLeer scheme belongs also to the class of limited schemes. The divergence of the indicator function alpha however is not used in interIsoFoam since a geometric reconstruction is used. It is used in interFoam. The same holds for the term div(phirb,alpha).
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile {
version 2.0; format ascii; class dictionary; location "system"; object fvSchemes;
} // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
ddtSchemes {
default Euler;
}
gradSchemes {
default Gauss linear;
}
divSchemes {
div(rhoPhi,U) Gauss limitedLinearV 1; div(phi,alpha) Gauss vanLeer; div(phirb,alpha) Gauss interfaceCompression; div(((rho*nuEff)*dev2(T(grad(U))))) Gauss linear;
}
laplacianSchemes {
default Gauss linear corrected;
}
interpolationSchemes {
default linear;
}
snGradSchemes {
default corrected;
}
fluxRequired {
default no; p_rgh; pcorr; alpha.water;
}
// ************************************************************************* //
Results
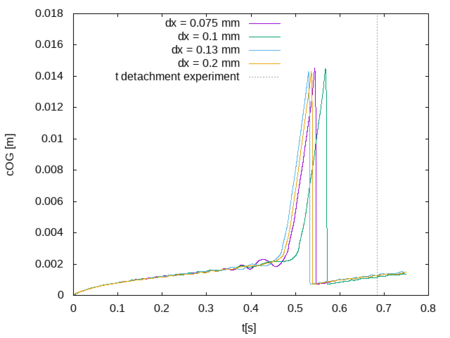
Varying the maximum grid size
The next figure shows the evolution of the center of gravity of the air phase. Note that the coded function which it used to calculate the value is described in https://wiki.openfoam.com/Bubble_growth_detachment_influence_BC_domain_size_by_Michael_Alletto. Four different cell sizes are simulated dx = dz = 0.2, 0.13, 0.1 and 0.075 mm. The evolution of the center of gravity of the air phase is very similar for all grid sizes considered: It is steady increasing until it shows a sharp gradient. This sharp gradient coincides with the detachment of the air bubble from the surface. The sharp decrease of the center of gravity represents the time step when the bubble leaves the domain. For the details of the flow picture see https://wiki.openfoam.com/Bubble_growth_detachment_influence_BC_domain_size_by_Michael_Alletto. It is evident that the detachment time shows no convergent behavior with decreasing grid size. A possible reason of a non-converging behavior of the solution with the grid size is that the curvature computation using the gradient of the volume fraction α is only zero-order accurate (see [3]). For this reason it is the preponderating error in the simulations where the surface tension place a crucial role effecting the flow behavior and the curvature is computed by the gradient of the volume fraction.
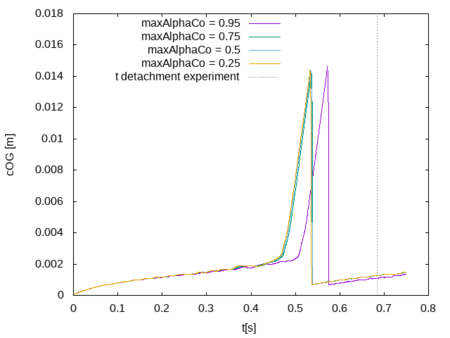
Varying the maximum Courant number
The next figure shows the evolution of the center of gravity of the air phase for different maximum interphase Courant number Coα. For the calculation of the interphase Courant number only the velocity of the advancing interphase is considered. For the details see FOAM\_APP/solvers/multiphase/VoF/alphaCourantNo.H. It is evident, that for a Coα <= 0.75 the evolution of the center of gravity of the air phase seems independent of the maximum interphase Courent number chosen.
According to the references cited in the review article of [2] the stability criterion for time explicit discretization of the surface tension force obeys following relation:
Δ is the grid size, σ the surface tension and ρ1 and ρ2 the densities of the two fluid involved. For the current setup we get a maximum time step size of 9.3 x 10-5 s with the above equation. Interestingly the solution remains stable for the current calculation which employ 2 to 3 times bigger time step for a maximum interphase Courant number of 0.95.
Lessons learned
- For the detachment time of the bubble no convergence regarding the grid size could be found. The reason is probly that the calculation of the curvature used in the expression of the surface tension force is zero order accurate if the gradient of the indicator function α is used [3].
- For a maximum interphase courant number of 0.75 the detachment time of the bubble becomes indipendent of the maximum Courant number used.
References
[1] Fadl Moukalled, L Mangani, Marwan Darwish, et al. The finite volume method in computational fluid dynamics, volume 113. Springer, 2016.
[2] Stéphane Popinet. Numerical models of surface tension. Annual Review of Fluid Mechanics, 50:49–75, 2018.
[3] Henning Scheufler and Johan Roenby. Twophaseflow: An openfoam based framework for development of two phase flow solvers. arXiv preprint arXiv:2103.00870, 2021.