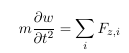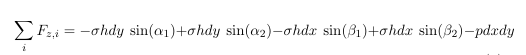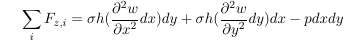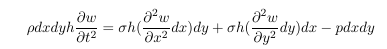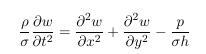Coupling a membrane with pretension to point displacement Michael Alletto

• contributor: Michael Alletto
• affiliation: WRD MS
• contact: click here for email address
• OpenFOAM versions: v2112
• Published under: CC BY-NC-ND license (creative commons licenses)

Go back to Collection by authors.

You can download the case https://gitlab.com/mAlletto/openfoamtutorials/-/tree/master/membranBCSend] here.

Introduction

In this small tutorial we will see how to couple two different physical problems in OpenFoam. In this specific case we will use the equation of motion of a membrane with pretension to impose the movement of the mesh at a given boundary. For membranes (which are very thin) the variation of the stress over the thickness is assumed constant. For this reason the governing equation reduce to a two dimensional problem. The equation of motion are described also in Wagner et al [3]. Part of the code presented later is taken from the work mentioned before. If a problem is purely two dimensional, OpenFoam offers the finite area method where a framework to discretize and solve 2D equation is offered. Summing up, we will see how to write advanced boundary condition for the 3D fields present in OpenFoam. In our specific case we will see how to derive a 2D differential equation for the membrane displacement w(x,y), solve it and use the solution to move the mesh at the boundary where our membrane boundary condition is applied. In order to deform the membrane, the pressure of the fluid is used.

Equation of motion

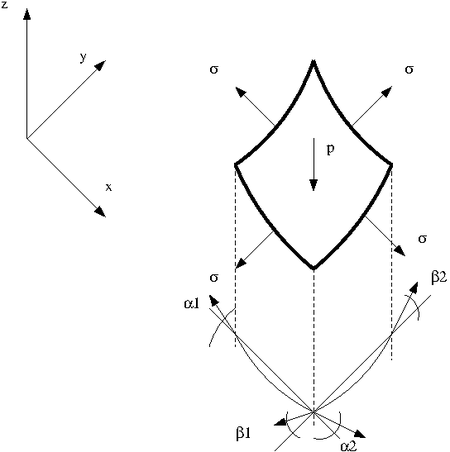
As first point in this tutorial we will briefly derive the equation of motion of a membrane subject to a prestress σ. Note that the derivation of the differential equation for a rod subject to an external force in z-direction and prestretched by a force S (the corresponding one dimensional case of a membrane subject to a prestess σ) can be found in Timoshenko [2] on page 352. Here we will see how to derive the equation for the two dimensional case. The next figure shows a sketch of the membrane subject to a prestress σ and an external pressure p.

The membrane has a thickness h. In order to derive the equation of motion one has to apply Newtons second law to an infinitesimal element with an extension dx and dy in a Cartesian coordinate system:

$w$ is the displacement of the membranes in z-direction and F_z,i are the forces in z-direction. Here we assume small displacements. Furthermore we assume that the only stress acting normal to the planes cutting the membrane is the prestress σ. σ is furthermore assumed to be constant. Making this assumptions we can write down the forces:

For small deformation the angles α₁, α₂, β₁ and β₂ are small and the sinus is almost equal to the tangent, i.e. sin (α₁) = tan ( α₁) = ∂w/∂x. Since the distance dx is small we can express tan (α₂) as function of tan (α₁): tan (α₂) = ∂w/∂x+ ∂tan (α₁)/∂x dx . The other angels can be determined in similar way. Inserting the expressions derived for the sinus in the above equation we get:

If we insert the above equation in the equation of motion and considering m = ρ dx dy h we get:

Finally we get after dividing by dx dy h σ:

Implementation

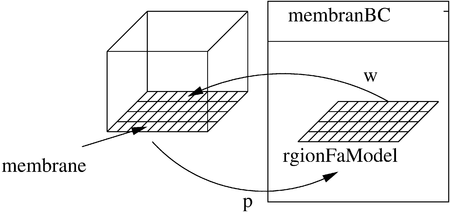
After having shortly derived the equation of motion, we will see how to implement a boundary condition which relates the displacement of the membrane w subject to the fluid pressure p to the deformation of the mesh. OpenFoam offers a nice framework to use the solution of two dimensional equation as boundary condition to a field of the 3D computational domain: The regionFaModel (see for more information). The finite area method discretizes and solves two dimensional differential equations. In our case, we will solve the equations for the membranes displacement w. The regionFaModel provides methods to map the solution of the fields of the three dimensional mesh to the two dimensional finite area mesh. In our case we will map the solution of the pressure p to the finite area mesh. A sketch of the procedure is shown in the next sketch. The membrane boundary condition holds an instance of a regionFaModel. The regionFaModel grabs the pressure from the membrane boundary and solves the equation for the displacement w of the membrane. The solution is taken from the membrane boundary condition and it is used the displace the mesh accordingly. Note that the displacement is applied in patch normal direction of the initial undeformed patch. This allows to the boundary condition to be applied to arbitrarily oriented surfaces.

After having worked out a rough idea of what our new boundary condition has to perform, it is useful to look for code in OpenFoam which does similar tasks, i.e. displace the boundary point field in wall-normal direction and apply a regionFaModel model to modify a field from the 3D domain at the boundary. The boundary condition surfaceDisplacement (see for more details ) displaces the points in wall-normal direction (see also the SnakeRiverCanyon tutorial). Looking at the regionFaModel (see src/regionFaModels) we see that there we have the KirchhoffShell model which solves a 2D equation for the displacement of the face centers using a thin shell model. (see the books [1,2] for the details). The Kirchhoff shell regionFaModel is used to obtain a coupling between the acoustic pressure p_a and the displacement of the shell w_s. The boundary condition for the acoustic pressure which uses the Kirchhoff shell can be found in src/regionFaModels/derivedFvPatchFields/vibrationShell.

In order to write the new boundary condition for the point displacement, we choose to copy the surfaceDisplacement boundary condition. It contains the method to displace the boundary points in wall normal direction. The patch wall-normal direction is obtained by following function call:

p.pointNormals()

The function pointNormals() of the object pointPatch returns the normal vectors at the boundary of the point field. In our new boundary condition we want to displace the boundary points in direction of the normal with the magnitude derived from the membrane equation of motion. Furthermore the boundary condition surfaceDisplacement is derived from a fixedValuePointPatchVectorField. This is the type we need to displace the boundary points by a given value.

The next step required in writing the new boundary condition, is to introduce the object responsible for solving the membrane equation into our new boundary condition. The vibrationShell boundary condition which is implemented in the current OpenFoam version does already the job. The only thing we need to do is to copy the methodology applied. As first point one has to define the smart pointer to the object responsible to solve the membrane equations in the header file:

       //- The finite-area region model
       typedef regionModels::membraneModel baffleType;

   // Private Data

       //- The membrane model
       autoPtr<baffleType> baffle_;

After that our membrane model has to be constructed in the constructor of the boundary condition:

 
   if (!baffle_ )
   {
       baffle_.reset(baffleType::New(mesh, dict_));
   }

Now that we have our regionFaModel available, we have to execute the membrane model to get the displacement at the boundary faces, interpolate the displacement $w$ of the membrane to the points of the mesh and apply the deformation in patch normal direction. This is performed in the following code snippet:

void Foam::membraneDisplacementPointPatchVectorField::updateCoeffs() {

   if (this->updated())
   {
       return;
   }
   
   baffle_->evolve();
   
   label patchID = this->patch().index();
   const areaScalarField& wMembran (baffle_->w());
   primitivePatchInterpolation patchInterpolator(baffle_->primaryMesh().boundaryMesh()[patchID]);
   scalarField pointnormalDisplacement = patchInterpolator.faceToPointInterpolate(wMembran);
   
   vectorField diplacement (pointnormalDisplacement*undeformedNormal_);
   
   this->operator==(diplacement);

   fixedValuePointPatchVectorField::updateCoeffs();

}

The function call evolve() basically solves the equation of motion of the membrane:

 
   faScalarMatrix wEqn
   (
       
       //fam::laplacian(w_) 
       laplaceUndeformed_
       ==
       fam::d2dt2(rho()/sigma0_, w_) - ps()/(sigma0_*h_)
       + faOptions()(rho()/sigma0_, w_, dimDensity/dimPressure*dimLength/sqr(dimTime))
   );

Note that the coefficients of the Laplacian are computed only once at the initial configuration. This is consistent with the linear theory which assumes small deformations and it turned out to be much more robust.

Test cases

In order to test our implementation we chose two simple test cases: a Hexahedron with a constant pressure inside and a Hemisphere in a uniform flow. The purpose of the hexahedron test case was to check if the analytical solution mentioned in Wagner et al [3] for a quadratic membrane subject to a constant pressure p can be retrieved. The hexahedron sides were initially aligned with the x-, y- and z-axis. Afterward it is rotated by 45° around the x-, y- an z-axis in order to show that the boundary condition developed can be applied to arbitrarily oriented boundary surfaces. The hemisphere in a uniform inflow is used to check if the boundary condition developed can be used to model fluid structure problems. Furthermore it is checked, if the boundary condition can be applied in principle to curved surfaces.

Hexahedron with a constant pressure

In this test case we had a hexahedron with a pressure p = 3 x 10⁵ N/m² , a pretension of σ = 1 x 10⁶ N/m², a thickness of h = 10^-2 m and a side length of the hexahedron of L = 0.01 m. For this configuration on has the analytical solution (see Wagner et al [3]) of w = 2.2 x 10^-3.

The next figure shows the initial configuration of the hexahedron on the left and the final configuration on the right. It is evident that the membrane model achieves a deformation of the mesh. The boundary condition can be applied to an arbitrarily oriented surface. The final displacement of w = 2.4 x 10^-3 is in reasonable agreement with the analytical result.

Hemisphere in uniform flow

In the next figure the configuration of the hemisphere test case is shown. The flow enters the domain from the left with a velocity of U = 0.1 m/s. A no slip condition is applied a the bottom surface and a zero gradient condition at the outlet. A slip boundary is applied at the side walls and at the top. The diameter of the sphere was D = 0.5 m. A pretension σ = 1.5 N/m² was applied to the membrane. For the pressure we had a constant value of zero at the outlet. The simulation is started with a static mesh at the beginning and the simulation was run for 150 s without allowing the mesh to deform. This is done in order that the simulation does not diverge at the beginning. After 150 s physical time, the deformation of the mesh is allowed and the simulation was run until 300 s physical time. At this time the results reached a steady state.

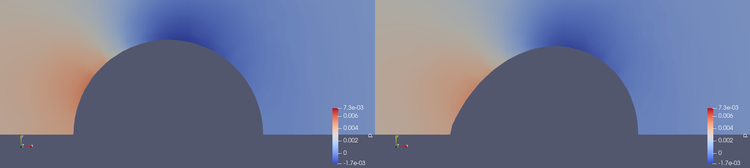
In the next figure the pressure distribution is shown at a slice through the middle of the hemisphere. The left figure shows the results right before the deformation of the mesh is started an the right figure shows the final results. The deformation is plausible: We have an inclination of the hemisphere in streamwise direction.

Lessons learned

• In OpenFoam is quite easy to glue together existing code to a new functionality

• The membrane boundary condition presented shows reasonable agreement with the analytical results for a flat squared surface

• The deformation obtained for a hemisphere in a uniform flow is plausible

References

[1] Junuthula Narasimha Reddy. Theory and analysis of elastic plates and shells. CRC press, 2006.

[2] Stephen Timoshenko, Sergius Woinowsky-Krieger, et al. Theory of plates and shells, volume 2. McGraw-hill New York, 1959.

[3] Simon Wagner, Manuel Münsch, and Antonio Delgado. An integrated openfoam membrane fluid-structure interaction solver. OpenFOAM R Journal, 2:48–61, 2022.