NACA0012 numerical schemes variation by Michael Alletto
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v2112
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to NACA0012 tutorial page.
NACA0012 Numerical schemes variation
Files can be downloaded here.
Numerical schemes variation
This section shows the results of the study of the discretization schemes used for the convective schemes. They are changed in the file system/fvSchemes. The following table shows the schemes which are analysis (note that a very good description of discretization schemes and small listings how they are implemented in OpenFOAM is found in the book ):
| name of scheme | brief description |
|---|---|
| upwind | first order upwind scheme |
| Gauss limitedLinear 0 | second order linear scheme with limiter switched off |
| Gauss limitedLinear 0.5 | second order linear scheme with limiter partially switched on |
| Gauss limitedLinear 1 | second order linear scheme with limiter switched on |
| Gauss linearUpwind limited | second order upwind scheme with a limiter |
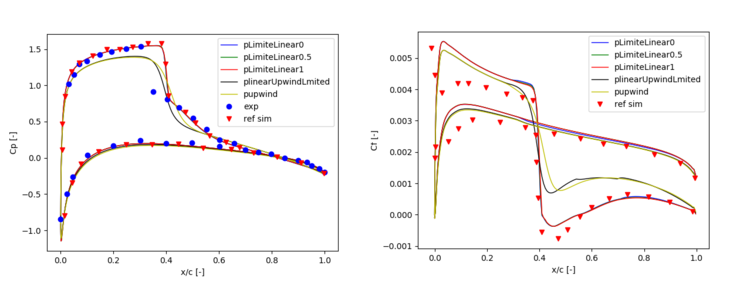
The next figure shows the influence of the numerical scheme adopted to discretize the divergence of the pressure in the pressure equation (the term fvm::div(phid, p)). It is the term (if it is big enough) which gives the pressure equation a hyperbolic character in case of high Mach numbers (see for the derivation of the pressure equation in case of compressible flows). If the term is small (for incompressible flows) the equation has a elliptic character. In principle this characteristic results in a pressure based flow solver able to treat flows at all speeds . Five different schemes are compared: The first order upwind Gauss labeled as pupwind, three different linear limited schemes with the limiter set to 0, 0.5 and 1 (the are labeled as pLimiteLinear0, pLimiteLinear0.5 and pLimiteLinear1 respectively) and a second order limited upwind scheme (labeled as plinearUpwindLmited).
From the figure below it can be seen that both upwind schemes (the upwind and linear upwind scheme) are too diffusive and smear out the pressure jump originated by the shock wave. The weaker shock results also in a vanishing of the recirculation bubble (see the Cf curve). All three version of the limited linear scheme (0 means the limiter is turned off and 1 means it is fully turned on) give almost identical results. For a discussion on the limiters which are introduced to the standard interpolation schemes in order that they satisfy the total variation diminishing (TVD) principle, see the book of .
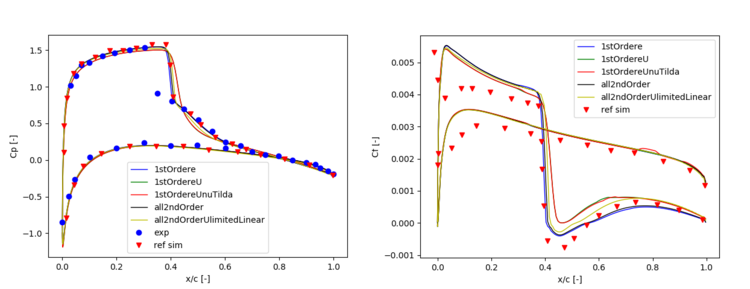
After the analysis of the discretization of the convective terms in the pressure equation, the convective therms in the other equations (energy, momentum and turbulence) are sequantially switched from a second order upstream (the case were all convective terms are discretized with a second order scheme is labeled as all2ndOrder) to a first order upstream. They are labeled as 1stOrdere, 1stOrdereU and 1stOrdereUnuTilda, respectively.
Regarding the other convective schemes shown in the next figure, the switching from second order to first order upwind leads to a change of the shock strength only when the convective term in the momentum equation is switched to first order.
Based on the study performed in this section, we can conclude that the initial settings of the tutorial lead to an accurate resolution of the shock wave and do not compromise the robustness (at least for the good quality mesh used in this tutorial).
References
[1] Fadl Moukalled, L Mangani, Marwan Darwish, et al. The �finite volume method in computational Fluid dynamics, volume 113. Springer, 2016.