The stationary droplet by Lionel Gamet
- contributor: Lionel Gamet
- affiliation: IFP Energies nouvelles, France
- contact: click here for email address
- OpenFOAM version: v2312
- Published under: CC BY-NC-SA license (creative commons licenses)
Go back to Multiphase modeling.
Contents
The stationary droplet
The starting cases case can be downloaded here:
- TwoPhaseFlow git repository
Reference OpenFOAM results of the stationary droplet can be found here.
Introduction
This case is a reference test case for Volume-of-Fluid (VoF) simulations. This benchmark configuration allows for quantitative measurements of the spurious currents appearing in VoF simulations. The case consists in a single static droplet in a quiescent liquid under zero gravity. It is a widely used test case in the literature, described by Popinet [1]. More details can be found in the iterature [1,2,3,4,5] and in the article in press of Gamet et al. [6].
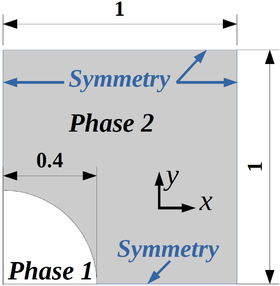
The 2D case setup is schematized in the Figure above. The phase 1 is the liquid, while the phase 2 is the gas. Both fluids have the same viscosity μ and density ρ. The volume fraction α is set to 1 inside the droplet near the bottom left corner, and to 0 outside. The density ρ and the surface tension σ between the two fluids are both taken as unitary constant values. The droplet has an initial diameter D_0 = 2R_0 = 0.8 m. Only a quarter of the 2D geometry is simulated in a domain of size 1x1 m. The droplet is placed at the bottom left corner of the domain. All boundary conditions are symmetries. This test case can easily be extended to 3D, where 1/8th of an initially spherical droplet is then simulated.
Ideally, the static droplet test case is not supposed to generate any velocity field and the pressure field should follow the Laplace pressure jump at the interface. However, parasitic velocities (also called spurious currents) can occur from a numerical imbalance between the discretization errors of the pressure gradient and surface tension terms.
Setting up the test case in OpenFOAM
This test case uses incompressible VoF solvers in OpenFOAM, namely interFoam or interIsoFoam solvers.
A uniform Cartesian grid built with blockMesh is used for the simulations. When running the sensitivity script, different grid levels and Laplace numbers are used (see section below). The droplet is initialized as a cylinder in 2D (as a sphere in 3D) using the setAlphaField utility.
In the fvSchemes file, a Crank-Nicolson second order time scheme with blending coefficient 0.9 is chosen. Gauss limitedLinearV 1 is used to treat the convective term, and Gauss vanLeer is used for the α convective term for MULES simulations. The Gauss linear scheme is used by default for all gradient terms.
In the fvSolution file, the GAMG implicit solver is used for pressure terms, while the smooth solver is used for the velocity. The PIMPLE algorithm uses 3 nOuterCorrectors in 2D (only 1 in 3D to save computational time) and 3 PISO correctors (nCorrectors=3). On other benchmark cases, it was found that momentumPredictor needed to be set to true to get a correct solution in terms of rising velocity and droplet circularity, in particular with isoAdvector. Both isoAdvector and MULES numerical parameters are present and appear separately in fvSolution, so that both interFoam and interIsoFoam can be run from the same input files.
The following reference time and velocity can be used to nondimensionalize results [5]:
We use the stability criterion of Popinet . The time step must be bellow the following upper limit:
Computations are done by default at a constant time step and up to t= 100 t_σ. In practice, the time step is set constant to:
with Co the Courant number as entered in controlDict and Δx=1/N, with N the number of grid cells along a coordinate direction. Writing interval for time directories is set every 10 t_σ. The constant time step is adjusted so that a writing interval corresponds to a whole number of time steps, multiple of 1000.
Post-processing quantities of interest are described in details in [1]. The main interest of this test case is to provide us with a measure of spurious currents. Those are obtained by recording minimum and maximum of velocity versus time overall the domain, thanks to a fieldMinMax functionObject. Of particular interest is the maximum of magnitude of velocity over the domain, which can be made dimensionless in terms of a maximum capillary number as:
The maximum capillary number is computed in the Allrun script, from the fieldMinMax output.
Other integral quantities of interest are the droplet volume and area, the droplet global velocity, the droplet circularity. All these quantities are computed through a coded functionObject inlined in the controlDict file, similar to the Hysing benchmark case. Please note that the droplet centroid of mass corresponds to the simulated portion (1/4th in 2D or 1/8th in 3D). The droplet centroid is thus not the origin. These integral results appear in the log file of the solver. We use a sampledIsoSurfaceCell object, defined as the isosurface α = 0.5, to compute the droplet area. We use volume integrals of the liquid fraction overall the computational domain to compute the droplet volume, centroid and velocity. A droplet equivalent diameter named D_A is computed from the droplet volume. A droplet equivalent diameter named D_B is computed from the droplet area. The circularity is defined in 2D as the ratio D_A/D_B. In 3D, we talk about sphericity defined as the ratio D_A^2/D_B^2. This number takes the value 1 at t=0 as the droplet is initialized as a perfect cylinder (or sphere in 3D).
Finally, the droplet shape and pressure profiles are output at writeTime frequency through surfaces and sets sampling functionObjects. The droplet shape is based upon the isosurface α=0.5. Both interpolated and constant iso droplet shapes are output.
Running the case
Allrun_sensitivity should be run first. This script is at a level above Allrun. It is used to prepare a grid size and Laplace sensitivity study (optionally density: By default, density is set to 1. Optionally, density can be set to 1, 10, 100, 1000 by changing line 21 in the script Allrun_sensitivity), for solvers interFoam, interIsoFoam, and also the enhanced version of isoAdvector by H. Scheufler, now partially integrated in the v2106 with the plicRDF reconstruction scheme, but also publicly available from the TwoPhaseFlow git repository. Allrun_sensitivity will create subdirectories ready to run, with a number of cells 25, 32, 42, 50, 64, 75, 100, 128 and 150.
The fluid viscosity is computed in Allrun_sensitivity from the Laplace number through the relation:
La numbers are taken as 1.2, 12, 120, 1200 and 12000.
You need to enter each generated subdirectory and type Allrun to start the corresponding computation. The grid is first constructed by running blockMesh. Then the setAlphaField utility is run to initialize the droplet as a cylinder. Finally, the application is run. Post-processing quantities of interest (droplet characteristics and spurious currents intensity) are extracted from the solver outputs through grep commands and simple computations.
For comparisons, OpenFOAM reference data are provided. Figures below show examples of spurious currents quantification in 3D (for a detailed description please hover over the figures). More details can be found in Gamet et al. [6]. Note that spurious currents intensities remain rather constant with time, and that the enhanced version of isoAdvector [7] brings lower amplitudes of parasitic velocities.
The prismatic/tetrahedral grid variant
A variant of the case setting is proposed on prismatic grids in 2D or tetrahedral grids in 3D. In that case, you can choose the grid generator tool (default to Pointwise) in Allrun_sensitivity. For this kind of grids, the default gradSchemes has been changed from Gauss linear to pointCellsLeastSquares. Besides, in the PIMPLE algorithm, nNonOrthogonalCorrectors was set to 1.
References
[1] S. Popinet: An accurate adaptive solver for surface-tension-driven interfacial flows," Journal of Computational Physics, vol. 228, no. 16, pp. 5838-5866, 2009.
[2] M. M. Francois, S. J. Cummins, E. D. Dendy, D. B. Kothe, J. M. Sicilian, and M. W. Williams: A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework," Journal of Computational Physics, vol. 213, no. 1, pp. 141-173, 2006.
[3] S. Popinet: A quadtree-adaptive multigrid solver for the serre-green-naghdi equations," Journal of Computational Physics, vol. 302, pp. 336-358, 2015.
[4] --: Numerical models of surface tension," Annual Review of Fluid Mechanics, vol. 50, pp. 49-75, 2018.
[5] T. Abadie, J. Aubin, and D. Legendre: On the combined effects of surface tension force calculation and interface advection on spurious currents within volume of fluid and level set frameworks," Journal of Computational Physics, vol. 297, pp. 611-636, 2015.
[6] L. Gamet, M. Scala, J. Roenby, H. Scheufler, and J.-L. Pierson: Validation of volume-of-Fluid OpenFOAM isoAdvector solvers using single bubble benchmarks," Submitted to Computers and Fluids, 2020.
[7] H. Scheufler and J. Roenby: Accurate and effcient surface reconstruction from volume fraction data on general meshes," J. Comp. Phys., vol. 383, pp. 1 - 23, 2019.
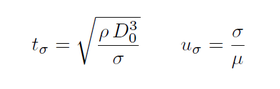
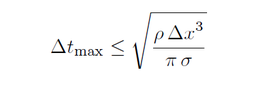
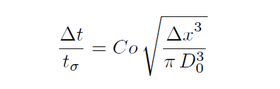
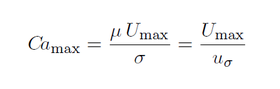
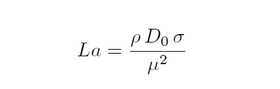
![Static droplet in 3D: Maximum capillary number over the computational domain for a hexahedral grid of size 323 versus nondimensional time, for different Laplace numbers. Solvers interFoam (MULES), interIsoFoam (iso-Alpha) and the enhanced version of isoAdvector by H. Scheufler [7] (plicRDF-5).](/images/thumb/2/23/StDrop3D_La_vary_CaMax_32_struct.png/750px-StDrop3D_La_vary_CaMax_32_struct.png)
![Static droplet in 3D: Maximum capillary number over the computational domain for a hexahedral grid of varying size versus nondimensional time, for Laplace number 1200. Solvers interFoam (MULES), interIsoFoam (iso-Alpha) and the enhanced version of isoAdvector by H. Scheufler [7] (plicRDF-5).](/images/thumb/3/37/StDrop3D_dx_vary_CaMax_La1200_struct.png/750px-StDrop3D_dx_vary_CaMax_La1200_struct.png)