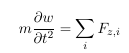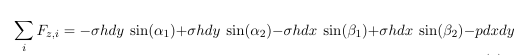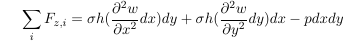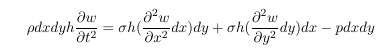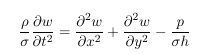Coupling a membrane with pretension to point displacement Michael Alletto

• contributor: Michael Alletto
• affiliation: WRD MS
• contact: click here for email address
• OpenFOAM versions: v2112
• Published under: CC BY-NC-ND license (creative commons licenses)

Go back to Collection by authors.

You can download the case https://gitlab.com/mAlletto/openfoamtutorials/-/tree/master/membranBCSend] here.

Introduction

In this small tutorial we will see how to couple two different physical problems in OpenFoam. In this specific case we will use the equation of motion of a membrane with pretension to impose the movement of the mesh at a given boundary. For membranes (which are very thin) the variation of the stress over the thickness is assumed constant. For this reason the governing equation reduce to a two dimensional problem. The equation of motion are described also in Wagner et al [3]. Part of the code presented later is taken from the work mentioned before. If a problem is purely two dimensional, OpenFoam offers the finite area method where a framework to discretize and solve 2D equation is offered. Summing up, we will see how to write advanced boundary condition for the 3D fields present in OpenFoam. In our specific case we will see how to derive a 2D differential equation for the membrane displacement w(x,y), solve it and use the solution to move the mesh at the boundary where our membrane boundary condition is applied. In order to deform the membrane, the pressure of the fluid is used.

Equation of motion

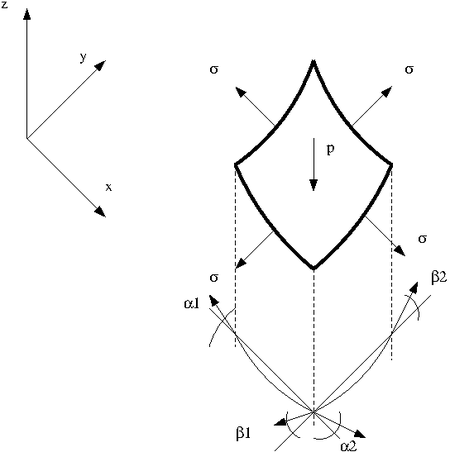
As first point in this tutorial we will briefly derive the equation of motion of a membrane subject to a prestress σ. Note that the derivation of the differential equation for a rod subject to an external force in z-direction and prestretched by a force S (the corresponding one dimensional case of a membrane subject to a prestess σ) can be found in Timoshenko [2] on page 352. Here we will see how to derive the equation for the two dimensional case. The next figure shows a sketch of the membrane subject to a prestress σ and an external pressure p.

The membrane has a thickness h. In order to derive the equation of motion one has to apply Newtons second law to an infinitesimal element with an extension dx and dy in a Cartesian coordinate system:

$w$ is the displacement of the membranes in z-direction and F_z,i are the forces in z-direction. Here we assume small displacements. Furthermore we assume that the only stress acting normal to the planes cutting the membrane is the prestress σ. σ is furthermore assumed to be constant. Making this assumptions we can write down the forces:

For small deformation the angles α₁, α₂, β₁ and β₂ are small and the sinus is almost equal to the tangent, i.e. sin (α₁) = tan ( α₁) = ∂w/∂x. Since the distance dx is small we can express tan (α₂) as function of tan (α₁): tan (α₂) = ∂w/∂x+ ∂tan (α₁)/∂x dx . The other angels can be determined in similar way. Inserting the expressions derived for the sinus in the above equation we get:

If we insert the above equation in the equation of motion and considering m = ρ dx dy h we get:

Finally we get after dividing by dx dy h σ:

Implementation

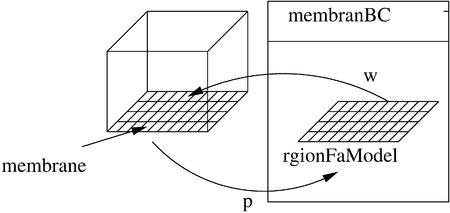
After having shortly derived the equation of motion, we will see how to implement a boundary condition which relates the displacement of the membrane w subject to the fluid pressure p to the deformation of the mesh. OpenFoam offers a nice framework to use the solution of two dimensional equation as boundary condition to a field of the 3D computational domain: The regionFaModel (see for more information). The finite area method discretizes and solves two dimensional differential equations. In our case, we will solve the equations for the membranes displacement w. The regionFaModel provides methods to map the solution of the fields of the three dimensional mesh to the two dimensional finite area mesh. In our case we will map the solution of the pressure p to the finite area mesh. A sketch of the procedure is shown in the next sketch. The membrane boundary condition holds an instance of a regionFaModel. The regionFaModel grabs the pressure from the membrane boundary and solves the equation for the displacement w of the membrane. The solution is taken from the membrane boundary condition and it is used the displace the mesh accordingly. Note that the displacement is applied in patch normal direction of the initial undeformed patch. This allows to the boundary condition to be applied to arbitrarily oriented surfaces.

After having worked out a rough idea of what our new boundary condition has to perform, it is useful to look for code in OpenFoam which does similar tasks, i.e. displace the boundary point field in wall-normal direction and apply a regionFaModel model to modify a field from the 3D domain at the boundary. The boundary condition surfaceDisplacement (see for more details ) displaces the points in wall-normal direction (see also the SnakeRiverCanyon tutorial). Looking at the regionFaModel (see src/regionFaModels) we see that there we have the KirchhoffShell model which solves a 2D equation for the displacement of the face centers using a thin shell model. (see the books [1,2] for the details). The Kirchhoff shell regionFaModel is used to obtain a coupling between the acoustic pressure p_a and the displacement of the shell w_s. The boundary condition for the acoustic pressure which uses the Kirchhoff shell can be found in src/regionFaModels/derivedFvPatchFields/vibrationShell.

In order to write the new boundary condition for the point displacement, we choose to copy the surfaceDisplacement boundary condition. It contains the method to displace the boundary points in wall normal direction. The patch wall-normal direction is obtained by following function call:

References

[2] Stephen Timoshenko, Sergius Woinowsky-Krieger, et al. Theory of plates and shells, volume 2. McGraw-hill New York, 1959.

[3] Simon Wagner, Manuel Münsch, and Antonio Delgado. An integrated openfoam membrane fluid-structure interaction solver. OpenFOAM R Journal, 2:48–61, 2022.