NACA0012 by Michael Alletto
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v2312
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to Collection by authors.
Transonic flow around a periodically pitching NACA0012 airfoil
The scope of this tutorial is to evaluate the capability of the solver rhoPimpleFoam to simulate a periodically pitching airfoil in a transonic flow at low angles of attack. At low angles of attack the flow remains attached or forms a closed recirculation bubble after the large pressure gradient induced by a shock wave without a massive flow separation. This keeps the complexity of the flow phenomena to a minimum.
The tutorial is divided into five different smaller tutorial to make things easier for the reader. They cover the following topics:
- Grid independence study
- Study of the discretization of the convective schemes
- Study of the turbulence model
- Study of the influence of the angle of attach and Mach number
- Apply the found setup to the moving airfoil
Introduction
Transonic means that part of the flow around the airfoil is subsonic and parts are supersonic. The Mach number far away of the airfoil Mainf < 1 is less than 1. Starting from far upstream the flow accelerates around the airfoil and becomes supersonic (Ma > 1) on one or both sides of the airfoil depending on its shape and incidence angle. Further downstream on the airfoil surface the flow becomes again subsonic by means of a nearly normal shock wave. See e.g. [1,7] for an overview on the topic.
Having a solver which is capable to simulate correctly the response of the flow to a periodically pitching airfoil at low angles of attack is the prerequisite to accurately predict more complicated phenomena like the structural response of helicopter blades to dynamic stall or the structural response of aircraft wings to buffeting flows. Dynamic stall is the transition from fully attached to fully stalled flows in periodically pitching airfoils. For a recent review on dynamic stall in compressible flows see [3]. The transonic buffet phenomena has its origin in the interaction between the shock and the separated shear layer: The interaction of a thin separated shear layer and the shock wave leads to a flow instability which manifests in a large amplitude and low frequency oscillation of the shock on the airfoil. Since the buffeting frequency lies in the low structural nodes this can lead to severe damage of the aircraft. For a recent review on this phenomena see [1,4].
The evaluation of the solver is done by means of a systematic validation. This systematic validation consists in following steps:
0) Needless to say that before tackling any problem a sorrowful literature review is indispensable in other to build up an expectation of the results one will obtain. This expectations will help as to critically evaluate the results preventing us to make too many errors or find some errors in the setup of the simulation more quickly.
1) The second step is to choose a simplified version of the problem to solve and do a systematic parameter study on this simplified problem: The parameter which we will analyze are the grid resolution, the numerical scheme and the turbulence model. For this scope we choose a fixed airfoil at given angle of attack α = 4° and given Mach number Ma = 0.725. The results are compared with experiments and other numerical results. The parameter variation and its comparison with experiments and other numerical results will show as the sensitivity of the solution on this parameter (grid resolution, numerical scheme of the convective terms and turbulence model) and its influence on the quality of the solution. Furthermore it will help as later to interpret the results of the more complex configuration which would have been rather difficult without this preliminary studies.
2) Check if the found setup gives acceptable results for other combinations of angle of attack and Mach number: This check ensures as the the setup we found with step 1 was not only luck but is applicable for a wider parameter space.
3) Simulate the more complex problem: In our case this will be the periodically pitching airfoil with the settings found in 1) and confirmed by step 2).
Setup
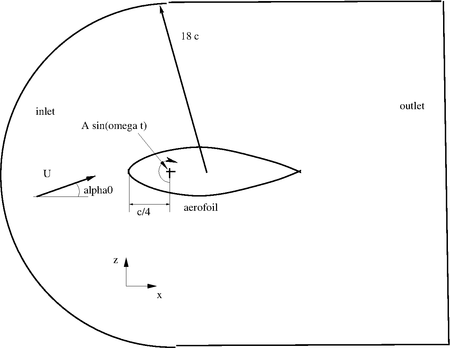
The setup of the simulation shown in the next figure. Note it is taken form the tutorial $FOAM_TUTORIALS/compressible/rhoPimpleFoam/RAS/aerofoilNACA0012 and adapted for the current purpose. A brief description of the solver rhoPimpleFoam and of the dictionaries used can be found here and here. Another one (actually the description of rhoSimpleFoam but except the transient term both solver are similar) can be found here. The solver rhoPimpleFoam together with a local time stepping (the entry localEuler has to be chosen in the fvSchemes dictionary for all transient terms) is used to simulate also the steady state simulations. The reason was that this combination was found to be more robust to obtain a converged steady solution compared to the rhoSimpleFoam solver.
The major change with respect to the afore mentioned tutorial was the enlarging of the domain in order that the distance from the airfoil to the outer boundaries is 18 chord length. The reason was to be more in line with simulation performed in the literature (see e.g. [5]). The constant angle of attach α0 is achieved by applying a z-component to the velocity at the inlet. For the cases with the oscillating airfoil, the pitching angle α(t) is changed with a sine function: α(t) = 0.0438 sin(42.5t) about a rotating point placed at quarter chord length. The angle is expressed in radiant. The Reynolds number is set to approximately Re = 1e7.
The boundary conditions applied are summarized in the next table. For the pressure at the inlet the freestreamPressure boundary conditions is used. It is an outlet-inlet condition that uses the velocity orientation to continuously blend between zero gradient for normal inlet and fixed value for normal outlet flow. The waveTransmissive boundary condition is an advective boundary condition where as wave speed the outgoing characteristic is taken. The freestreamVelocity velocity boundary condition switches between fixedValue and zeroGradient depending if the mass flux points inside (fixedValue) or outside (zeroGradient) the domain. The values at the inlet of the turbulence quantities (k,nuTilda, epsilon and omega) are set in a way to have already at the inlet a very small turbulent viscosity in order to resample the low turbulence intensity of the wind tunnel. The wall functions for epsilon and omega are derived by the assumption of equilibrium between production and dissipation (for the derivation see e.g. [2]). The same holds for the nutUSpaldingWallFunction (see also [6]) where a functional relation between y+ and U+ is derived which holds from the viscous sublayer to the log layer.
| inlet | outlet | aerofoil | |
|---|---|---|---|
| p | freestreamPressure | waveTransmissive | zeroGradient |
| U | freestreamVelocity | freestreamVelocity | noSlip |
| nuTilda | fixedValue | fixedValue | fixedValue |
| ε | inletOutlet | inletOutlet | epsilonWallFunction |
| ν | calculated | calculated | nutUSpaldingWallFunction |
| ω | inletOutlet | inletOutlet | omegaWallFunction |
In order to use the morphing mesh approach, only marginal modifications have to be made to the fixed mesh case. In order to let the solver know it has to deform the mesh, the file constant/dynamicMeshDict has to be present:
dynamicFvMesh dynamicMotionSolverFvMesh;
motionSolverLibs ( "libfvMotionSolvers.so" );
solver displacementLaplacian;
displacementLaplacianCoeffs
{
diffusivity inverseDistance 1(aerofoil);
}
The above file states that the applied displacement is relaxed with a Laplacian equation towards zero at the outer boundaries. The movement of the airfoil is specified in the file 0/pointDisplacement:
dimensions [0 1 0 0 0 0 0];
internalField uniform (0 0 0);
boundaryField
{
freestream
{
type fixedValue;
value $internalField;
}
wall
{
type angularOscillatingDisplacement;
axis (0 1 0);
origin (0.25 0 0);
angle0 0;
amplitude 0.0438;
omega 42.5;
value uniform (0 0 0);
}
#includeEtc "caseDicts/setConstraintTypes"
}
Grid independence study
This section shows the results of the grid independence study.
Study of the discretization of the convective schemes
This section shows the results of the study of the discretization schemes used for the 8https://wiki.openfoam.com/NACA0012_numerical_schemes_variation_by_Michael_Alletto convective schemes].
Study of the turbulence model
This section shows the results of the study of different turbulence models.
Study of the influence of the angle of attach and Mach number
This section shows the results of the study with different angles of attack as well as Mach numbers.
Moving airfoil
This section shows the results of a moving airfoil.
Lessons learned
In this tutorial we have seen a systematic procedure of how to evaluate the capability of the solver rhoPimpleFoam to simulated a moving airfoil in a transitional flow regime (both subsonic and supersonic regions are present). We started by evaluating the flow around a fixed airfoil by making a grid converged study. After that we analyzed the influence of the discretization schemes of the convective terms and finally we checked the influence of the turbulence model. After that we checked our setup for different Mach numbers and angles of attack. Only after doing this preliminary work we moved to the simulation of the moving airfoil. This systematic procedure allowed use to learn following lessons:
- A grid independence allows to find the best compromise between accuracy and computational cost for a given application
- The convective term in the pressure equation should be discretized with a central scheme in order to obtain an accurate resolution of the shock. For the convective schemes of the other equations a second order upwind scheme gives accurate results.
- In agreement with studies of the literature the Spalart-Allmaras model gives good results for the attached flow of a transonic airfoil
- Regarding the moving airfoil the qualitative picture of the alternating shock moving from the upper to the lower surface and vice versa is captured reasonably well.
- The distribution of the pressure coefficient over the airfoil agrees reasonably with the reference experiments.
- The hysteresis of the lift coefficient produced with the time varying angle of attack is too large compared with experiments. Reference simulations from the literature which fully resolved the wall got better agreement in contrast to the present wall modeled simulations. This observation gives a direction to go to improve the results.
- The change of the moment coefficient is too fast with respect to the angle of attack close to the maximum and minimum angle of attack. Again wall resolved simulations from the literature give better results for this quantity.
- The results from the first section of this tutorial (grid independence study, discretization study and turbulence model study) can be translated to the moving grid simulations: There are only minor differences between grid1 and grid2 and the Spalart-Allmaras and k-omegaSST model. If the convective therms in the pressure equation are discretized with a first order upwind scheme the shock is completely smoothed out.
References
[1] Oddvar O Bendiksen. Review of unsteady transonic aerodynamics: theory and applications. Progress in Aerospace Sciences, 47(2):135{167,2011.
[2] Jonas Bredberg. On the wall boundary condition for turbulence models. Chalmers University of Technology, Department of Thermo and Fluid Dynamics. Internal Report 00/4. Goteborg, 2000.
[3] Thomas C Corke and Flint O Thomas. Dynamic stall in pitching airfoils: aerodynamic damping and compressibility effects. Annual Review of Fluid Mechanics, 47:479-505, 2015.
[4] Nicholas F Giannelis, Gareth A Vio, and Oleg Levinski. A review of recent developments in the understanding of transonic shock buffet. Progress in Aerospace Sciences, 92:39-84, 2017.
[5] Daniella E Raveh. Numerical study of an oscillating airfoil in transonic buffeting flows. AIAA journal, 47(3):505-515, 2009.
[6] DB Spalding. A single formula for the law of the wall. 1961.
[7] H Tijdeman and R Seebass. Transonic flow past oscillating airfoils. Annual Review of Fluid Mechanics, 12(1):181-222, 1980.