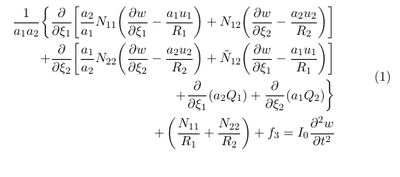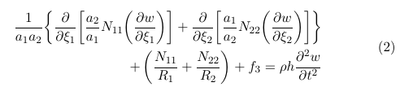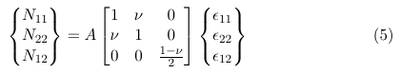Difference between revisions of "Coupling a simple nonlinear membrane to point displacement Michael Alletto"
| Line 42: | Line 42: | ||
[[File:simple_nonlinear_membrane_alletto_equation5.png|400px|center|equation 5]] | [[File:simple_nonlinear_membrane_alletto_equation5.png|400px|center|equation 5]] | ||
| + | |||
| + | &epsilon<sub>11</sub>, &epsilon<sub>22</sub> and &epsilon<sub>12</sub> are the longitudinal, the lateral and the shear strain, respectively. The constant A is defined as follows: | ||
| + | |||
| + | [[File:simple_nonlinear_membrane_alletto_equation6.png|400px|center|equation 6]] | ||
| + | |||
| + | E is the Young modolus, h is the thickness of the membrane and &nu is the Poisson ratio. | ||
==References== | ==References== | ||
Revision as of 12:41, 5 September 2023
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v2112
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to Collection by authors.
You can download the case https://gitlab.com/mAlletto/openfoamtutorials/-/tree/master/membranBCSend] here.
Introduction
In the tutorial https://wiki.openfoam.com/Coupling_a_membrane_with_pretension_to_point_displacement_Michael_Alletto we saw how to couple different physical models. In the before mentioned tutorial we coupled the equations of motion of a prestressed membrane with the displacement of the mesh. The membrane is deformed by the action of the pressure on the solid surface. The equations of motion for a prestressed membrane assume that the stress of the membrane is constant and does not change when the membrane is deformed. The question which arises is what is if we want to simulate a membrane which is in an initial undeformed and unstressed configuration and deforms by the action of the fluid pressure? How should we proceed to figure out what are the correct equations to be solved, what kind of assumptions has to be made to simplify the equation and how do we verify if our assumptions are correct? In this tutorial we will answer this question.
Equation of motion
The equations of motion for a curved thick membrane under the action of external forces can be found in Reddy [3] p. 421:
The above equation is described in a curvilinear coordinate system. x1 and x1 represent curved coordinates which follow the surface. N11 and N11 are the normal (membrane) forces per unit length. N12 represents the shear force parallel to the curved surface and Q1 and Q2 represent the shear forces normal to curved surface. R1 and R2 are the curvature radii and f3 is the external force acting normal to the plane. u1 and u2 are the displacements parallel to the curved surface and $w$ is the displacement normal to the curved surface. I0 = &rho h is the mass per unit surface. a1 and a2 are the scale factors (see e.g. https://mathworld.wolfram.com/ScaleFactor.html).
In our case we want only to consider the effect of the pressure on the membrane motion. Since the pressure always acts in surface normal direction, it reasonable to assume that the displacements parallel to the surface u1 and u2 can be neglected. For thin membranes the transverse shear forces Q1 and Q2 are usually set to zero (see \cite{reddy2006theory}). Since the pressure acts in surface normal direction is it also reasonable to assume that the membrane is not rotated parallel to the surface and hence also the shear force N12 can be neglected. With this assumption we obtain the following equation:
The first term in the above equation can be identified as the Laplacian in curvilinear grids (see e.g. http://sites.science.oregonstate.edu/~corinne/COURSES/ph461/laplacian.pdf). Therefore we can write down the above equation as:
The matrix N is defined as:
It evident that the term the first term on the left of the above equation can be seen as an diffusion equation with an anisotropic diffusion (see also [1])
The constitutive relations for a thin shell can be found in [3] p. 429:
&epsilon11, &epsilon22 and &epsilon12 are the longitudinal, the lateral and the shear strain, respectively. The constant A is defined as follows:
E is the Young modolus, h is the thickness of the membrane and &nu is the Poisson ratio.
References
[1] Fadl Moukalled, L Mangani, Marwan Darwish, et al. The finite volume method in computational fluid dynamics, volume 113. Springer, 2016.
[2] Draga Pihler-Puzović, Anne Juel, Gunnar G Peng, John R Lister, and Matthias Heil. Displacement flows under elastic membranes. part 1. ex- periments and direct numerical simulations. Journal of Fluid Mechanics, 784:487–511, 2015.
[3] Junuthula Narasimha Reddy. Theory and analysis of elastic plates and shells. CRC press, 2006.
[4] Stephen Timoshenko, Sergius Woinowsky-Krieger, et al. Theory of plates and shells, volume 2. McGraw-hill New York, 1959.