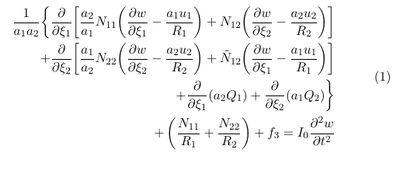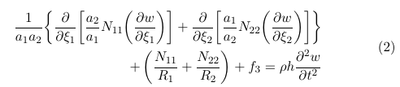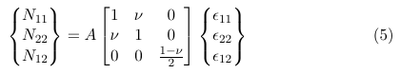Coupling a simple nonlinear membrane to point displacement Michael Alletto

• contributor: Michael Alletto
• affiliation: WRD MS
• contact: click here for email address
• OpenFOAM versions: v2112
• Published under: CC BY-NC-ND license (creative commons licenses)

Go back to Collection by authors.

You can download the case https://gitlab.com/mAlletto/openfoamtutorials/-/tree/master/membranBCSend] here.

Introduction

In the tutorial https://wiki.openfoam.com/Coupling_a_membrane_with_pretension_to_point_displacement_Michael_Alletto we saw how to couple different physical models. In the before mentioned tutorial we coupled the equations of motion of a prestressed membrane with the displacement of the mesh. The membrane is deformed by the action of the pressure on the solid surface. The equations of motion for a prestressed membrane assume that the stress of the membrane is constant and does not change when the membrane is deformed. The question which arises is what is if we want to simulate a membrane which is in an initial undeformed and unstressed configuration and deforms by the action of the fluid pressure? How should we proceed to figure out what are the correct equations to be solved, what kind of assumptions has to be made to simplify the equation and how do we verify if our assumptions are correct? In this tutorial we will answer this question.

Equation of motion

The equations of motion for a curved thick membrane under the action of external forces can be found in Reddy [3] p. 421:

The above equation is described in a curvilinear coordinate system. x₁ and x₁ represent curved coordinates which follow the surface. N₁₁ and N₁₁ are the normal (membrane) forces per unit length. N₁₂ represents the shear force parallel to the curved surface and Q₁ and Q₂ represent the shear forces normal to curved surface. R₁ and R₂ are the curvature radii and f₃ is the external force acting normal to the plane. u₁ and u₂ are the displacements parallel to the curved surface and $w$ is the displacement normal to the curved surface. I₀ = &rho h is the mass per unit surface. a₁ and a₂ are the scale factors (see e.g. https://mathworld.wolfram.com/ScaleFactor.html).

In our case we want only to consider the effect of the pressure on the membrane motion. Since the pressure always acts in surface normal direction, it reasonable to assume that the displacements parallel to the surface u₁ and u₂ can be neglected. For thin membranes the transverse shear forces Q₁ and Q₂ are usually set to zero (see \cite{reddy2006theory}). Since the pressure acts in surface normal direction is it also reasonable to assume that the membrane is not rotated parallel to the surface and hence also the shear force N₁₂ can be neglected. With this assumption we obtain the following equation:

The first term in the above equation can be identified as the Laplacian in curvilinear grids (see e.g. http://sites.science.oregonstate.edu/~corinne/COURSES/ph461/laplacian.pdf). Therefore we can write down the above equation as:

The matrix N is defined as:

It evident that the term the first term on the left of the above equation can be seen as an diffusion equation with an anisotropic diffusion (see also [1])

The constitutive relations for a thin shell can be found in [3] p. 429:

&epsilon₁₁, &epsilon₂₂ and &epsilon₁₂ are the longitudinal, the lateral and the shear strain, respectively. The constant A is defined as follows:

E is the Young modolus, h is the thickness of the membrane and &nu is the Poisson ratio.

Implementation

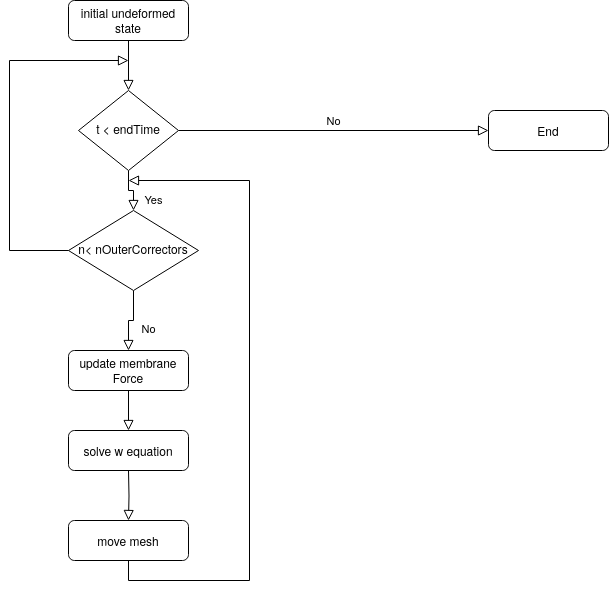
The algorithm proposed to solve the non-linear equation for the membrane (remember that the membrane force N is a function of the displacement w normal to the surface) is a simple predictor corrector algorithm. It is shown in the figure below. We start from the initial (undeformed) state. After that the time marching is started until the end time is reached. Within each time step the membrane equation can be solved several times by specifying a number of nOuterCorrectors in the fvSolution dictionary grater than 1. The solution procedure for the membrane equation is the following: 1) Update the membrane force: The membrane force depends on how much neighboring face centers are displaced relative to the initial stage. The magnitude of the displacement is retrieved from geometrical information, i.e. it is calculated from the distance between face centers adjacent to an edge and distances between the two points forming an edge. Since the mesh is moved at the end of the loop, the membrane force has to be updated at the beginning in order to retrieve the correct displacements. 2) Solve the membrane equation with the updated membrane force to get the displacement in surface normal direction w. 3) Move the mesh in the direction of the undeformed (initial) surface normal by the amount w calculated from the solution of the membrane equation. The three steps are repeated the number of times specified by the user in order to get a better estimation for the membrane force. Note that the flag MeshOuterCorrectors should be set to yes in the fvSolution dictionary in order to allow the mesh to move during the sub iterations within a time step. Otherwise the membrane force will not be updated during the sub iterations.

After having described the algorithm as a whole, we start with the description implementation of our equation with the anisotropic diffusion equation. As we know OpenFOAM uses a finite volume or in our case a finite area method to discretize the governing equation. If we integrate the anisotropic diffusion equation over the finite area and apply the Gauss-Green theorem we get:

In the above equation $dA$ represent the differential area element a $\mathbf{E}$ is the edge vector (in a finite volume discretization it corresponds to the surface area vector). The summation index $e$ means that we have to sum over the edges of the finite area element. With an additional manipulation of the above equation (see also \cite{moukalled2016} p. 255) we obtain the final discretized equation:

It is evident that the term N^T * E represent the projection of the membrane force in direction of the edge vector E

The anisotropic diffusion equation is implemented as follows:

fam::laplacian(normalForcef_, w_)

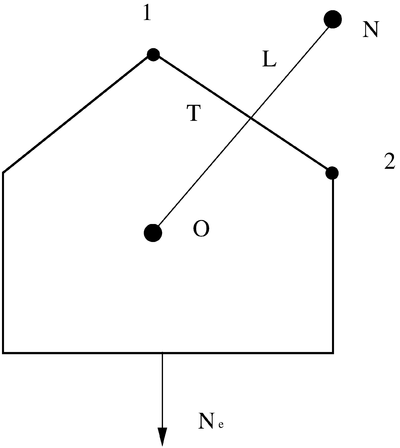
The edgeScalarField normalForcef_ represent the projection of the membrane force vector in direction of the edge vector E. In order to understand the current implementation, it is useful to have a look at the following figure. It represent a general polygonal cell. The cell consists in the cell center (labeled as O) and various neighbors (labeled as N). The distance between the owner cell center and the neighbor cell center is labeled as L. The length of the edge delimited by the points 1 and 2 is labeled as T. N_e represents the projection of the membrane force in direction normal to the cell edge.

References

[1] Fadl Moukalled, L Mangani, Marwan Darwish, et al. The finite volume method in computational fluid dynamics, volume 113. Springer, 2016.

[2] Draga Pihler-Puzović, Anne Juel, Gunnar G Peng, John R Lister, and Matthias Heil. Displacement flows under elastic membranes. part 1. ex- periments and direct numerical simulations. Journal of Fluid Mechanics, 784:487–511, 2015.

[3] Junuthula Narasimha Reddy. Theory and analysis of elastic plates and shells. CRC press, 2006.

[4] Stephen Timoshenko, Sergius Woinowsky-Krieger, et al. Theory of plates and shells, volume 2. McGraw-hill New York, 1959.