AMR supersonic sphere Re300 Ma1dot2 by Michael Alletto
- contributor: Michael Alletto
- affiliation: WRD MS
- contact: click here for email address
- OpenFOAM versions: v2312
- Published under: CC BY-NC-ND license (creative commons licenses)
Go back to Collection by authors.
Go back to Meshing.
Contents
AMR of the supersonic flow around a sphere at Re = 300 and Ma = 1.2
You can download the case file [1] here.
Introduction
In this tutorial we will simulate the compressible flow over a sphere at a Reynolds number Re of Re = 300 and a Mach number Ma = 1.2. We will also compare the resutls with the DNS of [4,5]. The purpose of this tutorial is twofold: First we want to evaluate the capabilities of the pressure based compressible solver rhoPimpleFoam to compute supersonic flows. The mesh is generated by snappyHexMesh to allow partial conclutions of the capability of the combination snappyHexMesh with the pressure based compressible solvers to compute the flow in complicated industrial relevant configurations. In the tutorial collection we already have two cases where we simulate the compressible transonic flow over a 2D wing (https://wiki.openfoam.com/NACA0012_by_Michael_Alletto ) and a 3D wing (https://wiki.openfoam.com/OneraM6_by_Michael_Alletto) and two tutorial of supersonic 2D cases (https://wiki.openfoam.com/Compressible_flows_by_Joel_Guerrero https://wiki.openfoam.com/Compressible_flows_by_Joel_Guerrero2). For this reason the simulation of a supersonic flow is the next logical step to check the performance of the compressible pressure based solver in OpenFOAM in a 3D geometry. The supersonic flow over a sphere is characterized by a bow shock wave in front of the sphere which influences the pressure distribution around the sphere and hence also the drag ( [4, 5]). This localized region with strong gradients away from the wall represents an ideal test case to show the advantages of the adaptive mesh refinement implemented in OpenFOAM. Note that a good description of how the mesh refinement in OpenFOAM works can be found in [2]. He also pointed out that the refinement of the wall layer generated by snappyHexMesh leads to errors. The same observation was also found here.
Set up
The next figure shows the simulated geometry. In order to save computational power, the full sphere is cut by two symmetry planes reducing the size of the domain by a factor of four. This will not exclude any possible solutions, since [4, 5] reported that for a Re = 300 and a Ma = 1.2 the flow around a sphere is steady and rotational symmetric. The Reynolds number Re is defined as Re = U∞d/ν∞ . U∞ is the inflow velocity, d the diameter of the sphere and ν∞ the dynamic viscosity at the inflow. The Mach number is defined as Ma = U∞/c∞ . c∞ is the speed of sound at the inflow. The flow at the inflow is directed in x-direction. The planes cutting the sphere are defined as symmetry plans. For all other planes a inflow-outflow boundary condition is applied. This means that for the velocity and energy if the flow is pointing inside the computational domain a fixed value boundary condition is applied and if the flow leaves the domain a zero gradient boundary condition is applied. For the pressure it is the way around: If the flow is directed inside the domain a zero gradient condition is used and if the flow is pointing outside the domain a fixed value condition is used. Since the flow at this Re is laminar, no other equations are solved. The extension of the computational domain was 20 diameters upstream and downstream of the sphere. In lateral directions it was also 20 diameters. Two different meshes (a coarse and fine one) are compared with each other. Furthermore two additional AMR simulations are performed: the two simulations differ in the threshold for which the mesh is refined.
Mesh generation
The next figures shows the meshing strategy adopted. The figures show the coarse mesh. The difference between the coarse and fine mesh is the innermost refinement level. For the coarse we use a level of 4 and for the fine one a level of 6. The purpose was to compare the solutions achieved on this two meshes with the solution achieved with the AMR starting with the coarse mesh and allowing a refinement of level 6. Five refinements regions are chosen to gradually increase the resolution from the coarsest level to the finest level around the sphere. The initial grid had hexagonal cells of 1.83 × 10−5 m side length. Note that it is very important to start with cells which are cubes to get a high wall layer coverage near the surface if wall layers are used. The fourth refinement level has a cell side length of 1.14 × 10−6 m and the sixth refinement level has a cell side length of 2.86 × 10−7 m. This strategy results in a mesh of approximately 23 000 cells for the coarse mesh and 130 000 cells for the fine mesh. Five layers are used to increase the wall normal resolution to capture the sharp velocity gradients near the wall. The layer coverage is 100%.
Simulation setup
The following listing shows the fvSolution dictionary. The transonic and the consistent switch is set to true. The transonic switch switches a divergence term in the pressure equation on. It transforms the pressure equation from an elliptical equation in case of a incompressible fluid to a hyperbolic equation in case of a compressible fluid. For details how the pressure equation is derived for compressible flows see the book of [3]. The consistent switch specifies that a SIMPLEC algorithm is used. A description of the algorithm SIMPLEC can be found in [3] or also https://openfoamwiki.net/index.php/SimpleFoam for the incompressible case. The implementation for the compressible case is very similar.
solvers {
p
{
solver GAMG;
smoother GaussSeidel;
tolerance 1e-6;
relTol 0.01;
}
pFinal
{
$p;
relTol 0;
}
"(rho|U|k|omega|e|nuTilda)"
{
solver PBiCGStab;
preconditioner DILU;
tolerance 1e-6;
relTol 0.1;
}
"(rho|U|k|omega|e|nuTilda)Final"
{
$U;
relTol 0;
}
}
PIMPLE
{
consistent yes; transonic yes; nCorrectors 2; nNonOrthogonalCorrectors 1; nOuterCorrectors 1; pMinFactor 0.1; pMaxFactor 4;
}
relaxationFactors {
equations
{
".*" 1;
}
}
Regarding the fvSchemes dictionary has to be said that it is important to use a linear scheme for all convective terms to accurately capture the shock. A detailed discussion can be found in https://wiki.openfoam.com/NACA0012_numerical_schemes_variation_by_Michael_Alletto Since we want to compute the steady solution we use a localEuler scheme for the time derivative. The following listing shows the thermophysicalProperties which defines the thermodynamic package used. Note that a small description of the entries of the thermophysicalProperties dictionary can be found in https://www.openfoam.com/documentation/user-guide/thermophysical.php or https://cfd.direct/openfoam/user-guide/v6-thermophysical/. What is important for the tutorial is that we used a pure mixture, the specific heat capacity cp (not to be confused with the pressure coefficient) is constant, a ideal or perfect gas is used as equation of state and that the internal energy is solved in the energy transport equation. Regarding the transport properties (i.e. the kinematic viscosity μ) a Sutherland relation is used to describe its change with the temperature. The DNS of [4] also used a Sutherland relation to describe the temperature dependence of the dynamic viscosity. In the bow shock we have large temperature gradients and a temperature dependent viscosity seams to be more appropriate than a constant one. The constants of the Sutherland model are taken for dry air. For a discussion on the topic see https://curiosityfluids.com/2019/02/15/sutherlands-law/.
thermoType {
type hePsiThermo; mixture pureMixture; transport sutherland; thermo hConst; equationOfState perfectGas; specie specie; energy sensibleInternalEnergy;
}
mixture {
specie
{
molWeight 28.9;
}
thermodynamics
{
Cp 1007;
Hf 0;
}
transport
{
As 1.4792e-06;
Ts 116;
}
}
The next listing shows the dynamicMeshDict for the two AMR simulations performed. For the refineInterval setting we choose a value of 50 until the time step 0.015. After that we set the value to 10000 to keep the mesh unchanged. The purpose was to achieve a really steady state solution. I observed some wiggles in the signal of the drag force until the end of the simulation if the refineInterval setting is kept the same throughout the simulation. The update of the file refineInterval is done in the controlDict via the function timeActivatedFileUpdate. As field upon the refinement is performed we choose the custom made field refineField. It is defined in the controlDict via a coded function object. It is defined as follows: refineField = |∆p|Vcell1/3 ShieldwallLayer . A very similar refinement field was also used by [1, 6]. [1] also shielded the wall layer while [6] did not use this shielding. [6] stated that the function |∆p|Vcell1/3 is an indicator of the numerical error. Vcell is the volume of the cell and ShieldwallLayer is a shielding switch which is zero at a wall normal distance corresponding the the thickness of the wall layers added by snappyHexMesh. The shielding of the wall layers has to be performed since otherwise the AMR produces a fatal error. The interval where a refinement of the grid is performed is defined by the parameters lowerRefineLevel and upperRefineLevel. Two value of the parameter lowerRefineLevel are used: One with 7000 and one with 5000. The values are found by try and error in order to obtain a trade off between no refinement at all (very high values of lowerRefineLevel) and a too fine grid which leads to high computational costs (very low values of lowerRefineLevel). The parameter maxRefinement defines up to which refinement level the refinement is performed. The value 6 is chosen to be equal to the innermost refinement region of the fine mesh.
dynamicFvMesh dynamicRefineFvMesh;
// How often to refine
- include "refineInterval"
//refineInterval 10;
// Field to be refinement on field refineField;
// Refine field inbetween lower..upper lowerRefineLevel 7000.0; upperRefineLevel 1.0e20;
// Have slower than 2:1 refinement
nBufferLayers 1;
// Refine cells only up to maxRefinement levels maxRefinement 6;
// Stop refinement if maxCells reached maxCells 500000;
// Flux field and corresponding velocity field. Fluxes on changed // faces get recalculated by interpolating the velocity. Use 'none' // on surfaceScalarFields that do not need to be reinterpolated. correctFluxes (
(phi none) (nHatf none) (rhoPhi none) (alphaPhi0.water none) (ghf none) (alphaPhiUn none)
);
// Write the refinement level as a volScalarField dumpLevel true;
The next listing shows the coded function object which is used to define the field refineField which is used to refine the mesh.
refineFunc
{
libs ("libutilityFunctionObjects.so");
type coded;
// Name of on-the-fly generated functionObject
name refineFunction;
writeControl writeTime;
executeControl timeStep;
codeOptions
#{
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/OpenFOAM/lnInclude
#};
codeInclude
#{
#include "volFieldsFwd.H"
#include "hexMatcher.H"
#};
codeData
#{
#};
codeRead
#{
#};
codeExecute
#{
hexMatcher hex;
static autoPtr<volScalarField> refineField_;
// check in into database in order to be visible for the
// refinement
if(!refineField_.valid())
{
Info << "Creating refineField_" << nl;
refineField_.set
(
new volScalarField
(
IOobject
(
"refineField",
mesh().time().timeName(),
mesh(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh(),
dimensionedScalar("refineField", dimPressure, scalar(0.0))
)
);
}
volScalarField refineFlag
(
IOobject
(
"refineFlag",
mesh().time().timeName(),
mesh(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh(),
dimensionedScalar("zero", dimless, 0.0)
);
// Ma
const volScalarField& fieldToUse = mesh().lookupObject<volScalarField>("p");
Info << "mesh nCells " << mesh().nCells() << endl;
Info << " refineField size " << refineField_().size() << endl;
for (label celli = 0; celli < mesh().nCells(); celli++)
{
refineFlag[celli] = 0.0;
scalar xc = mesh().C()[celli].component(0);
scalar yc = mesh().C()[celli].component(1);
scalar zc = mesh().C()[celli].component(2);
scalar r = sqrt(xc*xc + yc*yc + zc*zc);
//flag out non hex cells and boundary layers which cause errors
if ( r > 1.3*5.67E-06 )
{
refineFlag[celli] = 1.0;
}
}
volScalarField cellSize
(
IOobject
(
"cellSize",
mesh().time().timeName(),
mesh(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh(),
dimensionedScalar("zero", dimLength, 0.0)
);
cellSize.ref() = pow(mesh().V(),1./3.);
refineField_() = mag(fvc::grad(fieldToUse)) * refineFlag * cellSize;
//* Foam::pow(mesh().V(),1./3.);
#};
codeWrite
#{
#};
}
The most important part is the check in of the field refineField into the database:
static autoPtr<volScalarField> refineField_;
// check in into database in order to be visible for the
// refinement
if(!refineField_.valid())
{
Info << "Creating refineField_" << nl;
refineField_.set
(
new volScalarField
(
IOobject
(
"refineField",
mesh().time().timeName(),
mesh(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh(),
dimensionedScalar("refineField", dimPressure, scalar(0.0))
)
);
}
Without this step the AMR would not find the field in the database. The key point here is that we created a static (globally visible) smart pointer to the volScalarField refineField_. If the field does not exist it is created. This is of course done only once per simulation. In all other time steps when the function object is executed the if statement does nothing since the field already exists in the database.
The shielding of the wall layer is done by the following code lines:
for (label celli = 0; celli < mesh().nCells(); celli++)
{
refineFlag[celli] = 0.0;
scalar xc = mesh().C()[celli].component(0);
scalar yc = mesh().C()[celli].component(1);
scalar zc = mesh().C()[celli].component(2);
scalar r = sqrt(xc*xc + yc*yc + zc*zc);
//flag out non hex cells and boundary layers which cause errors
if ( r > 1.3*5.67E-06 )
{
refineFlag[celli] = 1.0;
}
}
The field refineFlag is set to 1.0 everywhere except in a region of radius 1.3 sphere radii around the origin of the coordinate system. Since looking at the log file of snappyHexMesh we know the wall layer is 0.3 radii thick, this region corresponds to the extension of the wall layers. For other geometries then a sphere, the wall distance can be used to shield the wall layers. Most of the turbulence models have a member function to assess this field (it is called y()).
Results
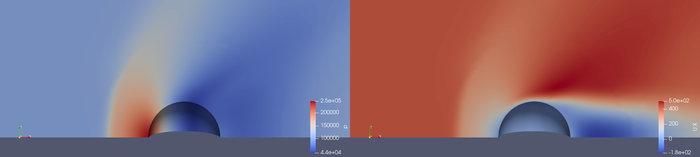
The next figures show a front view of the pressure distribution and the x- velocity. From the pressure distribution the bow shock in front of the sphere is clearly visible. Further downstream a expansion region and a further recompression region is present. From the x-velocity distribution we can observe the presence of a large recirculation region behind the sphere. In general the overall flow picture agrees qualitatively well with the reference DNS of [4, 5].
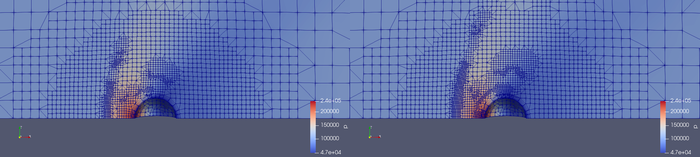
The next figures show the front view of the meshes obtained for the case where the lowerRefineLevel was set to 7000 (left) and to 5000 (right). We see that the regions which are refined are essentially the same: The region of the bow shock, the region close to the stagnation point except the wall layer region which is shielded by the custom made function and the region of the expansion waves above the sphere. We can observe that for the lower refinement level this refinement regions become bigger and finer resolved. Unfortunately the region in the wake is not refined. If we want to refine also this regions, we have to employ a different refinement criteria which involves also the velocity gradient which are high especially at the border of the recirculation region. In fact, [1] used a refinement criteria which is base not only on the gradient of the pressure but also on the gradient of the Mach number.
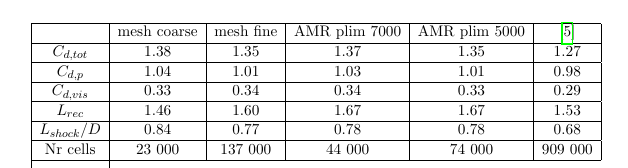
The next table shows the comparison of the total drag coefficient Cd,tot, the pressure induced drag coefficient Cd,p , the viscous stress induced drag coefficient Cd,vis , the length of the recirculation bubble Lrec and the shock stand off distance Lshock between the current simulation and the DNS of [5]. The drag coefficients are calculated by normalizing the corresponding forces by the dynamic pressure at infinity and the projected area of the quarter sphere (i.e. a quarter of the area of a circle). Unfortunately [5] did not mention how they calculated the shock stand off distance. For this reason I took the distance from the sphere on the x-axis where the pressure exceeds 10% of the ambient value to calculate this value. The length of the recirculation region is the distance behind the sphere on the x-axis where the x-velocity switches sign. The python scripts to calculate the values are included in the tutorial material. Also here the agreement of the simulations with the reference DNS of [4, 5] is quite good. We also see that for this integral quantities the AMR leads to values which are very close to the simulations with the fine grid. The final number of cells is however only a fraction of the number of cells used for the fine grid.
Lessons learned
- The agreement with the reference DNS of [5] is quite good
- AMR is a very good method to refine the mesh only there where a high resolution is required. The definition of an adequate refinement criteria however is far from trivial.
- The application of AMR on a grid generated with snappyHexMesh is possible if the wall layer is excluded from the refinement. The refinement of the wall layer caused the simulation to crash.
References
[1] Jeremy Hanke and Martin Krcmar. Adaptive mesh refinement of hypersonic shock and wake structures in simcenter star-ccm+. In AIAA AVIATION 2020 FORUM, page 3227, 2020.
[2] Saumitra Vinay Joshi. Adaptive mesh refinement in openfoam with quantified error bounds and support for arbitrary cell-types. 2016.
[3] Fadl Moukalled, L Mangani, Marwan Darwish, et al. The finite volume method in computational fluid dynamics, volume 113. Springer, 2016.
[4] T Nagata, T Nonomura, S Takahashi, and K Fukuda. Direct numerical simulation of subsonic, transonic and supersonic flow over an isolated sphere up to a reynolds number of 1000. Journal of Fluid Mechanics, 904, 2020.
[5] Takayuki Nagata, Taku Nonomura, Shun Takahashi, Yusuke Mizuno, and Kota Fukuda. Investigation on subsonic to supersonic flow around a sphere at low reynolds number of between 50 and 300 by direct numerical simulation. Physics of Fluids, 28(5):056101, 2016.
[6] J Sinclair and Xinjun Cui. A theoretical approximation of the shock standoff distance for supersonic flows around a circular cylinder. Physics of Fluids, 29(2):026102, 2017.